数学クイズ『モンティ・ホール問題』
2016.09.25
みなさんこんにちは、吹田教室の長川です。
今回は初回ということで、ひとつクイズを出してみたいと思います。
「モンティ・ホール問題」という言葉を聞いたことがあるでしょうか。
一時期全米で話題になった問題で、当時正確に答えを導けたのは「世界で一番高いIQの持ち主」のマリリンさん(IQ200!)だけでした。
みなさんもIQ200に挑戦してみて下さい。
「モンティ・ホール問題」
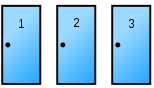
このように、1、2、3の三つのドアがあります。
三つのうち、二つのドアにはヤギが入っています(はずれです)。
残る一つのドアには100万円が入っています!
あなたには一度だけドアを開ける権利があります。
頑張って100万円をゲットしましょう。
ただし前提として、100万円のドアとヤギのドアはランダムに決まるものとします。
あなたは「1」のドアを選んでみることにしました。
この時ヒントが与えられます。
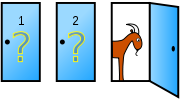
あなたが選ばなかったドア(この場合は「2」と「3」)の中から、ヤギのドアを一つ教えてもらえるのです。
仮にここでは「3」のドアがヤギだと教えてもらったとします。
(もちろん常に「3」がヤギというわけではなく、あくまでも一例です)
この時、あなたはどちらのドアを開けたらいいのでしょうか
A.「1」のドアのほうが100万円が当たりやすい
B.「2」のドアのほうが100万円が当たりやすい
C.「1」も「2」も当たりやすさは同じ
さて、考えてみて下さい。
(中学三年生以上の人は、確率を使って考えてみよう)
下にスクロールした先に答えがあります。
さて、どうだったでしょうか。
IQ200の問題ということで、色々考えてみてくれたかもしれません。
正解は、
B.「2」のドアほうが100万円が当たりやすい
でした。
しかも、
「1」よりも「2」のドアのほうが『2倍』も当たりやすいのです。
びっくりしましたか? 少しイメージと違ったと思います。
何故「2」のドアのほうが当たりやすいのか。
何故その当たりやすさが2倍も違うのか。
その答えは、次回解説したいと思います。