プロの講師陣による完全個別指導

こんにちは。修優舘の道明です。

少し暑くなって来ましたね。

皆さん暑さに負けずに頑張って下さい。

 

さて、早速ですが、

 

今日は三平方の定理です。

 

下記の図形を見て下さい。

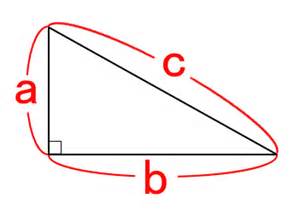
このような直角三角形がある時、

c²=b²+a²

 

が成り立ちます。

 

これを「三平方の定理」といいます。

 

こんな問題が出ます。

 

【問題】

「a=7,C=25　の時のｂの値は❔」

 

こんな問題、皆さんならどうやって解きますか？

 

えーと・・・c²=b²+a²

だから、

 

25の二乗＝b²+7の二乗だから・・・

25の二乗＝625　7の二乗＝49

625＝b²+49　ここから移項して

b²＝625－49

  b²＝576

 

b²＝だから・・・576を素因数分解して・・・

ｂ＝24！

 

こんな解き方してませんか？

こんな計算方法では、計算がややこしくなる上、計算ミスをしてしまいます。

 

それでは、解きましょう

 

まず、

b²＝c²－a²

と移行します。

するとなにやら因数分解できそうな形になります。

 

因数分解します。

b²＝（ｃ＋a）×（ｃ－a）になります。

a=7,ｃ=25　を代入します。

b²＝（25＋7）×（25－7）

b²＝32×18

になります。ここで32×18をせずに・・・

32＝２×16

18＝２× 9

に分解しときます。

b²＝２×2×16×9となり

 

16は4の二乗、9は3の二乗なので、

b²＝２×２×４×４×３×3

ｂ＝2×４×3

ｂ＝24

となります。

 

どうですか？

25の二乗の計算、素因数分解の計算がなくなり、計算ミスは必ず減ります。

 

ではもう一問

 

【問題】

同じ図で　ｂ＝24、C＝25の時のaの値は❔

 

もうできますね。

a²=c²−b²

=（25－24）×（25+24）

= 1×49

＝49

a=7

 

今回は暗算でできますね。

 

次回は泉丘教室の小学生に非常に評判の良い

算数マジックを紹介したいと思います。

 

それでは、皆さん体調に気を付けて頑張って下さい。